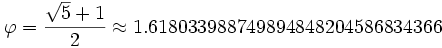عدد طلایی

نسبت طلایی
نسبت طلایی یا Golden Ratio که با علامت phi نمایش داده می‌شود، عددی است که هزاران سال است که بشر از آن استفاده می کند. بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که بنظر می رسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد این نسبت الهام بخش بسیاری از هنرمندان و معماران اروپایی شده و بسیاری از نقاشان نیز از این نسبت در آثار خود استفاده کرده اند که از آن جمله می توان به نقاش بزرگ لئوناردو داوینچی اشاره کرد. همچنین خطاطان ایرانی نیز از این نسبت بهره برده اند.
این نسبت نه تنها توسط معماران و مهندسان، برای طراحی استفاده می شود، بلکه در طبیعت نیز کاربردهای بسیاری دارد. مثلا این نسبت در قسمت های مختلف بدن انسان رعایت شده، مانند نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج

نسبت طلایی چیست؟
پاره خطی را در نظر بگیرید و فرض کنید که آن را به گونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید.
اگر شما معادله a2=a*b+b2 را در نظر بگیرید و بجای b یک قرار دهید، مقدار a مساوی 1.61803399 خواهد شد.
در شكل زیر تمام خط A قطعه بزرگترB و قطعه سوم C است .
نسبت قسمت A به قسمت B برابر است با نسبت قسمت B به قسمت C
این در صورتی است كه نسبت B به C و نسبت A به B برابر با 1.618

مستطیل طلایی
مستطیلی وجود دارد که بر مبنای عدد طلایی کار می‌کند. این مستطیل به مستطیل طلایی معروف است. در زمانهای قدیم هنرمندان یونانی به خوبی ریاضی دانان، مستطیل زیبایی می شناختند كه از نظر هنری عرض 1 و طول X داشت، در این مستطیل هر وقت مربعی به ضلع 1 را از آن جدا كنند باز همان مستطیل با همان نسبتهای مستطیل اصلی باقی می‌ماند .
چون مستطیل جدید عرض 1-X و طول 1 دارد و چون نسبت ضعلهای دو مستطیل با هم برابر است، پس داریم :
حالا اگر در معادله ی بالا برحسب X حل كنیم، ریشه ی مثبت معادله همان عدد طلایی است

کاربرد عدد طلایی در معماری
این نسبت از گذشته در ساختمان سازی استفاده فراوانی می شد که برای نمونه می‌توان اهرام مصر را نام برد.
اهرام مصر یکی از قدیمی ترین ساخته های بشری است که در آن هندسه و ریاضیات بکار رفته شده است. مجموعه اهرام Giza در مصر که قدمت آنها به بیش از 2500 سال پیش از میلاد می رسد یکی از شاهکارهای بشری است که در آن نسبت طلایی بکار رفته است
مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا" 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادله فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند phi2=phi+b2 خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا" عدد طلایی را با phi نمایش می دهند).
طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا" معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد. مطلب جالب دیگر این است كه اگر قطر این هرم را به دوبرابر ارتفاع ان تقسیم كنیم جواب عدد پی (3.14) خواهد بود .
مثال دیگر در بنای پارتنون در یونان وجود دارد .برای ساخت این بنا كه در 440 قبل از میلاد ساخته شده است از مستطیل طلایی استفاده شده است:

نسبت طلایی در خوشنویسی
استاد میرعماد با پالایش خطوط پیشینیان و زدودن اضافات و ناخالصی‌ها از پیکره نستعلیق و نزدیک کردن شگرف نسبت‌های اجزای حروف و کلمات، به اعلا درجه زیبایی یعنی نسبت طلایی رسید و قدمی اساسی در اعتلای هنر نستعلیق برداشت. با بررسی اکثریت قاطع حروف و کلمات میرعماد متوجه می‌‌شویم که این نسبت به عنوان یک الگو در تار و پود حروف و واژه‌ها وجود دارد و زاویه ۴۴۸/۶۳ درجه که مبنای ترسیم مستطیل طلایی است، در شروع قلم گذاری و ادامه رانش قلم، حضوری تعیین کننده دارد. این مهم قطعاً در سایه شعور و حس زیبایی‌شناسی وی حاصل آمده، نه آگاهی از فرمول تقسیم طلایی از دیدگاه هندسی و علوم ریاضی. میرعماد این نسبت‌ها را نه تنها در اجزای حروف بلکه در فاصله دو سطر و مجموعه دو سطر چلیپاها و کادرهای کتابت و قطعات رعایت می‌‌کرده است.
نسبت طلایی در طبیعت
به اشکال شبیه چشم روی بدن پروانه که علامت گذاری شده است،توجه کنید.نسبت فواصل طولی و عرضی این علائم یک نسبت طلائی است.
نسبت طلایی در بدن انسان
دانشمندان گذشته نیز از نسبت طلایی استفاده های زیادی کرده اند. به عنوان مثال لئوناردو داوینچی در ترسیم نقاشی معروف خود از بدن انسان از نسبت طلایی بهره گرفته است.
در بدن انسان مثالهای بسیار فراوانی از این نسبت طلایی وجود دارد. در شکل زیر نسبت M/m یک نسبت طلایی است که در جای جای بدن انسان می توان آنرا دید. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج
نسبت فاصله شانه تا بالای سر به اندازه سر
نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا
اینها تنها چند مثال از وجود نسبت طلایی در بدن انسان بود که بدن انسان را در حد کمال زیبایی خود نشان می دهد

• فراكتال هاى هندسى
ساده ترين نوع فراكتال، فراكتال كانتور است. پاره خطى به طول يك واحد در نظر بگيريد و طول آن را به سه قسمت تقسيم كرده و قسمت وسطى را حذف كنيد. حالا دو تا خط داريم كه طول آنها يك سوم طول اوليه است. همين عمل را با هر كدام از اين پاره خط ها هم انجام مى دهيم. يعنى طول هر كدام را ثلث مى كنيم و قسمت وسطى را حذف مى كنيم. مى توان با كامپيوتر برنامه اى نوشت كه اين عمليات را چندين بار پياپى انجام دهد. اگر اين عمليات را بى شمار بار انجام دهيم (كارى كه از عهده كامپيوتر خارج است) شكلى به دست مى آيد كه مجموعه كانتور نام دارد. اگر به كل شكل نگاه كنيم، ساختارى مى بينيم كه تا بى نهايت ادامه دارد. اگر به سمت راست يا چپ خط دوم شكل نگاه كنيم، ساختارى مى بينيم كه باز هم تا بى نهايت ادامه يافته و در عين حال، كاملاً شبيه شكل كلى است. چنين ساختارهايى كه هر جزء آن با كل مجموعه يكى است و فقط در مقياس (Scale) تفاوت دارند را ساختارهاى خودمتشابه Self-similar مى گويند.
يكى از مشهورترين انواع فراكتال ها توسط «هلگ فون كخ» در سال ۱۹۰۴ طراحى شد، در اين نوع فراكتال، ابتدا يك پاره خط به طول يك واحد درنظر مى گيريم و آن را به سه قسمت تقسيم مى كنيم. سپس به جاى ضلع وسط دو ضلع مثلث متساوى الاضلاع را قرار مى دهيم. و اين كار را همين طور ادامه مى دهيم. فراكتال كخ نيز يك نوع فراكتال خودمتشابه است. اگر اين عمل را روى اضلاع يك مثلث متساوى الاضلاع انجام دهيم، شكل بسيار زيبايى به دست مى آيد كه «دانه برف كخ» نام دارد.
فراكتال سرپينسكى يك فراكتال هندسى است. اگر مثلث وسطى يك مثلث متساوى الاضلاع را حذف كنيم و براى همه مثلث هاى باقى مانده هم اين عمل را تا بى نهايت ادامه دهيم، مجموعه زيبايى از مثلث هاى پر و خالى به وجود مى آيد كه فراكتال سرپينسكى به دست خواهد آمد. در همه انواع فراكتال هاى خودمتشابه براى تبديل هر جزء به كل يا اجزاى كوچكتر، بايد همه ابعاد به يك مقياس بزرگ شوند. اما نوع ديگر فراكتال را خود الحاقى (Self-Affine) مى گويند. در اين نوع از فراكتال ها براى تبديل شدن به مقياس بزرگ تر بايد شكل در هر راستا به ضرايب مختلفى بزرگ نمايى شود. DNA زنجيره طويلى از اسيدهاى نوكلئيك است كه اطلاعات ژنتيكى را در خود ذخيره كرده است. اسيدهاى نوكلئيك دو دسته اند، پريدين و پريميدين. اگر در طول يك زنجيره DNA براى هر پريدين يك واحد به بالا برويم و براى هر پريميدين يك واحد به پائين، نمودارى به دست مى آيد كه داده هاى زيادى به ما مى دهد. به اين نمودار ولگشت DNA (DNA Walk) مى گويند. ولگشت هاى DNA نمونه هاى خوبى براى فراكتال هاى خودالحاقى هستند. اكثر ساختارهاى فراكتالى در طبيعت مثل ريشه هاى گياهان يا شاخه هاى درخت ها، ساختارهاى خوشه ها و كهكشان هاى كيهان، رشد يك سطح، سوختگى هاى روى كاغذ، شكستگى هاى DVDها و ساختارهاى زمين شناسى به خصوص اشكال زيبايى كه در غارها مشاهده مى شود، خواص فراكتالى خود الحاقى دارند. يكى از زيباترين نمونه هاى فراكتالى گل كلم است.

برای دریافت نرم افزار Fractal Explorer اینجا کلیک کنید

کسی بوده لیسانس ریاضی داشته.دنبال کار میگشته ولی هیچ کاری پیدا نمی کرده.یه روز یه آگهی میبینه که از طرف شهرداری بوده برای استخدام.
میره شهرداری.میپرسن مدرکت چیه میگه لیسانس.میگن :مابرای یه کارگرشهرداری حقوق یه لیسانسو نمی دیم.مابیسواد می خوایم.
طرف بر میگرده خونه.فردا میره شهرداری میگه من بیسوادم استخدامش میکنن.
مسئول های شهرداری میگن کارگرهامون نباید خیلی بیسواد باشن برای همین براشون کلاس میزارن.
سر یکی از کلاس های ریاضی معلم یه مستطیل پای تخته میکشه به طرف می گه بیا مساحتشو حساب کن(طول وعرضش هم نوشته بوده)
میره پای تخته هرچی فکر میکنه فرمول مساحت یادش نمیاد.می خواسته مساحتشو با انتگرال حساب کنه ولی میگه اینجوری همه می فهمن لیسانسه.
همون موقع موبایل معلمه زنگ میزنه و معلمه میره بیرون.
طرف به اونایی که نشستن میگه برسونین
اونایی که نشسته بودن میگن:
-انتگرال بگیر
-انتگرال بگیر

فراکتال و کاربرد آن در موسیقی

همواره افرادی بر این عقیده بوده اند که موسیقی از دسته ی علوم ریاضی بشمار میرود و گرچه نوع بیان موسیقی و ریاضی با یکدیگر متفاوت بوده اما روح و حقیقتی که در موسیقی وجود دارد، در ریاضیات قابل مشاهده است؛ بنابراین همواره وجود داشته اند افرادی که بخواهند ریاضیات و موسیقی را به زبان دیگری تعریف کرده و یا از این علوم قدرتمند جهت غنا بخشیدن به دیگری استفاده کنند. آن طور که در تاریخ آمده شروع بررسی موسیقی از دیدگاه ریاضی به یونان باستان بازمیگردد و فیثاغورثیان در پانصد سال قبل از میلاد، اولین افرادی بودند که فواصل موسیقی را متناسب با اعداد بیان کرده و ارتباط موسیقی و ریاضیات را توجیه کردند.
از آن زمان تا کنون بکارگیری و بررسی ریاضیات در موسیقی در طی دورانها و زمانهای مختلف پیگیری شد و در حال حاضر نیز ریاضیات بطور گسترده در تشریح، آنالیز و ساخت موسیقی استفاده میشود؛ مثلآ از روابط ریاضی در الگوریتمهای آهنگسازی برای یافتن صداهای مناسب برای کوک کردن سازها کمک میگیریم و یا در جای دیگر برای ساخت یک آهنگ از ریاضی استفاده میشود. باید گفت این موارد نمونه های کوچکی از کاربردهای ریاضیات در موسیقی است. سیستمهایی که رابطه موسیقی و ریاضی را شرح میدهند اساسآ در قرن بیستم توسعه یافتند.
از این میان میتوان به سیستم آهنگسازی جوزف شیلینگر (Joseph Schillinger) و متد ساخت آهنگ از اولیور مسیان (Olivier Messiaen) در سال 1940 اشاره کرد. از آن زمان به بعد متدهای جدیدتر در این زمینه بیشتر بر اساس فراکتالها بودند که با استفاده از آنها افق تازه ای برای ساخت نغمات جدیدتر برای آهنگسازان ایجاد شد.
واژه Fractal از کلمه لاتین Fractus یعنی (شكسته) گرفته شده و در لغت به معنی سنگي است كه به شكل نامنظم شكسته شده باشد. یکی از مهمترین خصوصیات فراکتالها خود متشابه بودن آنهاست به این معنی که فراکتالها از اجزایی تشکیل شده اند که هر جزء در آن شبیه به کل شکل میباشد؛ شکل گل کلم و سرخس معروفترین مثالهایی است که برای تعریف فراکتال ارائه میشود.
برای ملموس تر شدن موضوع اجازه دهید کمی از این هندسه زیبا را در اطرافمان بیابیم: ساختارهای فراکتالی در بسیاری از ساختارهای طبیعی مثل ساختمان دانه های برف، شكل كوه ها، ابرها و شكل ريشه، تنه و برگ درختان، رویش بلورها در سنگهای آذرین، شبکه آبراه ها و رودخانه ها، رسوبگذاری الکتروشیمیایی، رویش توده باکتریها و سیستم عروق خونی وغیره دیده میشوند و با آنها میتوان پدیده های طبیعی بسیاری را تشریح، تفسیر و پیش بینی کرد.
موارد کاربرد فراکتالها آنچنان زیاد است که حتی نمیتوان لیستی از آن ارائه داد. چند مورد از کاربرد های روزمره با فراکتال ها: مثلآ در کامپیوتر (برای فشرده کردن تصاویر یا پردازش تصاویر)، فیزیک (آنتن های گوشی موبایل)، پزشکی (برای تفسیر نوار قلبی و پیش بینی رفتار بدن)، معماری و شهرسازی، اقتصاد، شیمی، پیش بینی وضع هوا، زمین شناسی و حرکت گسل ها و بسیاری از مواد دیگر؛ همچنین میتوان رد پای فراکتال ها را در خلق آثار هنری جست و با استفاده از آنها ایده های بدیع و زیبایی خلق نمود.

واژه فرکتال درسال 1976 توسط رياضيدان لهستاني به نام بنوئيت مندلبرات وارد دنياي رياضيات شد.

واژه فركتال به معناي سنگي است كه به شكل نامنظم شكسته شده باشد.

فراکتال ها

نظريه ي بي نظمي (آشوب) يک مفهوم رياضياتي محسوب مي‌شود که شايد نتوان خيلي دقيق آن را تعريف کرد، اما مي‌توان آن را نوعي اتفاقي بودن همراه با قطعيت دانست؛ قطعيت آن به خاطر آن است که بي‌نظمي دلايل دروني دارد و به علت اختلالات خارجي رخ نمي‌دهد، اتفاقي بودن آن هم به دليل آن است که رفتار بي‌نظمي، بي‌قاعده و غير قابل پيش‌بيني است. اين تئوري که در حيطه علوم تجربي، رياضيات، رفتار شناسي، مديريت، جامعه شناسي و ... وارد شده‌ و باعث تغيير در نوع ديدگاه بشر به حل مسائل غير قابل پيش‌بيني شده‌است. انگاره اصلي و کليدي تئوري آشوب اين است که در هر بي‌نظمي، نظمي نهفته‌است. به اين معنا که نبايد نظم را تنها در يک مقياس جستجو کرد و پديده‌اي که در مقياس محلي، کاملاً تصادفي و غير قابل پيش‌بيني به نظر مي‌رسد، چه بسا در مقياس بزرگتر کاملاً پايا و قابل پيش‌بيني باشد.