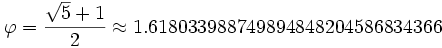|
***( fraktal )*** ( ریاضیات عبارتست از اثبات بدیهی ترین چیز به نا بدیهی ترین روش ممکن ) درباره وبلاگ باسلام خدمت بازدید کننده ی گرامی. این وبلاگ در مورد بحث های ریاضی ست.امیدوارم این وبلاگ مورد پسند و رضایت شما قرار گیرد. آخرین مطالب
آرشيو وبلاگ نويسندگان شنبه 21 بهمن 1391برچسب:, :: 22:30 :: نويسنده : نا شناس
افشای بخشی از راز نسبت طلایی کاربرد نسبت طلایی در معماری معبد پارتنون در آتن. بزرگترین مستطیل که تمامی نمای معبد را درون خود جای داده است، یک مستطیل طلایی است. به همین ترتیب نسبت طول ستونها به ارتفاع تاج معبد و نسبت عرض جزءِ مستطیلیِ تاج به ارتفاع جزءِ مثلثیِ آن، نسبتی طلایی است در این میان هزاران سال است ثابتی منحصربفرد و جذاب را یافتهایم که در گوشهگوشه جهانمان رخنه کرده و ردپایش از ترمودینامیک سیاهچالههای فضایی گرفته تا زادآوری منظم خرگوشها و حتی اهرام مصر کشیده شده است؛ ثابتی موسوم به "عدد فی" یا "عدد طلایی". در حدود ۳۰۰ سال پیش از میلاد، ریاضیدان برجستهی یونان باستان؛ اقلیدس، در فصل چهارم از کتاب معروفش «اصول»، که تا پیش از این قرن، پرخوانندهترین کتاب جهان غرب پس از انجیل بود؛ اینچنین نوشته است:«یک پارهخط مستقیم را میتوان به دو قسمت کوچک و بزرگ آنچنان تقسیم نمود که نسبت طول پاره خط به جزء بزرگ، برابر با نسبت طول جزء بزرگ به کوچک باشد". او با حل جبری این مسأله دریافت که مقدار چنین نسبتی همواره معادل نصف مجموع مجذور ۵ و یک؛ یا ۱.۶۱۸۰۳۳۹۸۸۷ میباشد؛ عددی گنگ1 همچون پی، که بعدها «عدد فی» نامیده شد. فی، نخستین حرف از نام «فیدیاس»، پیکرتراش زبدهی یونان باستان است که به احتمال زیاد این نسبت عددی را دهها سال پیش از اقلیدس، در شیوهی هنریاش لحاظ میکرده است. فی، صرفاً بعنوان یک نماد هندسی، اسیر ذهن پویای ریاضیدانان نماند و اندکی بعد، پا به جهان پیرامونمان نهاد و صاحبنظران هر حوزه از علم آن روز را در شگفتی تمام فروبرد. هر اندشمندی با دریافتی که خود از اعجاز بیپایان این عدد داشت، به دنبال واژهای بود که به بهترین نحو از زیبایی و شکوه ذاتی آن عدد حکایت کند. «لوییجی پاچیولی»، ریاضیدان ایتالیایی، این نسبتِ عددی را «نسبت ملکوتی» نام نهاد و «مارتین اهم» آلمانی، در کتاب خود از آن با عنوان «نسبت طلایی» یاد کرد.به هر حال این نسبت باستانی، هر روزه خود را اغلب در حوزههایی که هیچ انتظاری از آنها نمیرود، به شکل بدیعی آشکار میسازد و بر انبوه سؤالات بیپاسخ ما میافزاید. مارپیچهای لگاریتمی و تنوع حیرتانگیز مصادیق طبیعی آنها، نمونهی بارزی از اعجاز عدد فی است. برای ترسیم یک منحنی لگاریتمی ایدهآل از نوع طلایی، کافی است یک چهارضلعی طلایی رسم کنید؛ بگونهای که نسبت طول به عرض آن، معادل این عدد باشد.مقایسهی منحنی طلایی موجود در ساختار مارپیچ یک فسیل آمونیت (جانداری آبزی شبیه حلزون اما با ابعاد متغیر و گاهاً غولپیکر که میلیونها سال پیش میزیسته است) ،و نیز یک کهکشان مارپیچی پس از آن از درون مستطیل، یک مربع جدا کنید. حال، مستطیل اولیه به یک مربع و یک مستطیل کوچکتر که اتفاقاً اضلاع آن هم از نسبت طلایی پیروی میکنند، تقسیم شده است. روند مربعسازی را همچنان برای مستطیلهای کوچکتر و کوچکتر ادامه دهید.حال، درون هر مربع از گوشهها یک ربع دایره رسم کنید که شعاعش معادل ضلع مربع میزبان باشد. با ادامه این روند؛ مارپیچی گردابگون به دست میآید که با کمال شگفتی، دقیقاً مشابه مارپیچهای صدف یک حلزون، بازوهای یک کهکشان مارپیچی، ابرهای درهمتنیدهی طوفانهای هولناک گرمسیری و مارپیچ اتمی یک مولکولDNAاست. «یوهانس کپلر»، منجم صاحبنام آلمانیتبار، در نیمهی اول قرن هفده میلادی و دهها سال پیش از کشف کهکشانهای مارپیچی گفته بود: «سنت هندسهی باستان، دو میراث بزرگ برای ما به یادگار گذاشت. نخست، قضیهی فیثاغورث و دیگری راز تقسیم یک پارهخط به نسبتهای بیشینه و میانه. اگر اولی مثل حلقهی طلا ارزشمند باشد، دومی گوهری نایاب و گرانقیمت است که زینتبخش هر جواهری خواهد بود.» بسیاری از معماران و هنرمندان کهن، نسبت طلایی را دستمایه کار خود ساخته و دست به خلق آثاری شگرف و ماندگار زدهاند. از معروفترین نمونههای آنها، تابلوهای «مونالیزا» و «مرد ویترووین»، اثر لئوناردو داوینچی و بنای «پارتنون» یونان، مربوط به ۲۴۶۰ سال پیش است. جالب اینجاست که چنین نسبتی در اعضای بدن هر انسان سالمی نیز خود را نمایان میسازد. بعنوان مثال، در یک چهرهی زیبا و ایدهآل، نسبت فاصلهی چشمها تا لب به فاصلهی لب تا چانه، و نیز نسبت عرض چشمها و بینی به عرض لب، معادل عدد طلایی است. راز این «نسبت ملکوتی» چیست؟ چندی پیش «آدریان بژان»، یکی از یکصد مهندس مکانیک برتر جهان و استاد دانشکدهی فنی دانشگاه دوک در ایالت کارولینای شمالی، نظریهای ارائه داد که احتمالاً از راز نقش عدد فی در هنر و زیستشناسی، پرده برمیدارد.مطابق با این نظریه، چشمان ما نمایی که چارچوبی به شکل یک مستطیل طلایی داشته باشد را با حداکثر سرعت ممکن، مورد بررسی و کنکاش خود قرار میدهند. پیروی از طراحی ویژهای که پیوند گسستناپذیر بینایی و ادراک یک انسان معمولی را امکانپذیر ساخته، سادهترین روشی است که به فرآیندهای جریانی (همچون فرآیند تشکیل دلتای یک رودخانه و یا فرآیند تردّد هوا در مسیر شُشهای جانداران)، امکان تحول هرچهبهتر و بقای بیشتر جریان را میدهد. بژان، در سال ۱۹۹۶ این گفته را تحت عنوان «قانون ساختاری» ارائه داد و آخرین نمونهی کاربرد آن نیز، در آخرین شمارهی آنلاین «نشریهی بینالمللی طراحی، طبیعت و اکودینامیک» مورد بررسی قرار گرفته است.بژان میگوید: «با نگاهی به آنچه که توسط افراد بسیاری طراحی و یا ساخته شده است، چنین نسبتهایی را همهجا خواهید دید. خوب میدانیم که چشمان ما با بررسی افقی یک نما (از چپ به راست و بالعکس)، اطلاعات کارآمدتری را نسبت به بررسی عمودی آن (از بالا به پایین و بالعکس) به دست میآورد.»وی مدعی است که جهان، چه از دید انسانی که به یک اثر هنری مینگرد و چه از دید غزالی که دشت پیش رویش را تحت نظر دارد، اصولاً به جهت افقی گرایش دارد. برای یک غزال، خطر اصولاً از جهات افقی او را تهدید میکند؛ نه بالا یا پایین. از اینرو گسترهی دید چنین جانوری نیز بصورت افقی نمو یافته است. به ادعای بژان، با دید بهتر و تحرک سریعتر بود که جانوران باهوشتر شدند. وی در ادامه میگوید: «با رشد و بهبود اندام بینایی، جانوران احتمال بروز خطر از روبرو و اطراف را به حداقل رسانده و بدینگونه جریان تحولی جانوران زمین، ایمنتر و مؤثرتر شد. (از این طریق) جریان جمعیت جانوری، گذرگاههای ایمن و مؤثری را برای بقای خود ایجاد کرد.» از دیدگاه بژان، قوای بینایی و ادراک، وجودی متحدند که با هم تکامل یافته و در نحوهی گذار تحولی خود نیز درونمایهای یگانه و مشترک دارند. تکامل اندامهای دیداری با هدف ارتقای بازدهی مسیرهای انتقال اطلاعات از چشمها به مغز، مشابه همان روشی است که انشعابات عصبی سلولهای مغزی ما را در طول هزارههای متمادی به نحو مطلوبی متحول ساخت. با وجود آنکه راز نسبت طلایی، کورهراهی به سمت شناخت این جنبه از طراحی طبیعت به روی ما گشوده است؛ اما بژان همچنان افقی دورتر را مینگرد. به اعتقاد وی نقش یگانگی قوههای بینایی، ادراک و پویایی یک انسان در تحول او، مشابه همان مسیری است که جانوران زمین از نوعی به نوع دیگر متحول شده و فرگشت یافتند. پدیدهی نسبت طلایی، به درک نحوهی همکاری فاکتورهایی چون «الگو» و «تنوع»؛ بعنوان اجزای گسستناپذیر و ضروری در مسیر تحول طبیعی، کمک شایان توجهی خواهد نمود.با این وجود، هر چند این نظریه را میتوان عاملی برای توجیه نقش بارز نسبت طلایی در آثار هنرمندان باستان دانست؛ اما نمیتوان به آسانی دلیل تشابه حیرتآور مارپیچهای طلایی یک کهکشان مارپیچی به طول دهها هزار سال نوری را با منحنی منقّش بر صدف یک حلزون چندسانتمیتری توجیه نمود. شاید پاسخ به این پرسش همچون ماهیت بسیاری از ثوابت فیزیکی در هالهای از ابهام بماند و شاید هم یادآور گفتهای از آلبرت اینشتین باشد: «زیباترین تجربههای زندگی نهفته در رویارویی با پررمز و رازترین پدیدههای طبیعت است ... کسیکه از این اسرار سربهمُهر به وجد و هیجان نیاید و یا آن را هیجانانگیزترین تجربهی بشر نداند، بهتر از شمعی خاموش و روحی مرده نیست.» پنج شنبه 19 بهمن 1391برچسب:, :: 12:16 :: نويسنده : نا شناس
لئوناردو داوینچی در ترسیم نقاشی معروف خود از بدن انسان از
بهره گرفته است.
در بدن انسان مثالهای بسیار فراوانی از این نسبت طلایی وجود دارد. در شکل زیر نسبت M/m یک نسبت طلایی است که در جای جای بدن انسان می توان آنرا دید. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج
نسبت فاصله شانه تا بالای سر به اندازه سر
نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا اینها تنها چند مثال از وجود نسبت طلایی در بدن انسان بود که بدن انسان را در حد کمال زیبایی خود نشان می دهد. نسبت طلایی یک شنبه 15 بهمن 1391برچسب:, :: 18:29 :: نويسنده : نا شناس
• فراكتال هاى هندسى یک شنبه 15 بهمن 1391برچسب:, :: 1:15 :: نويسنده : نا شناس
کسی بوده لیسانس ریاضی داشته.دنبال کار میگشته ولی هیچ کاری پیدا نمی کرده.یه روز یه آگهی میبینه که از طرف شهرداری بوده برای استخدام. جمعه 13 بهمن 1391برچسب:, :: 17:49 :: نويسنده : نا شناس
دو خط موازی به هم نمی رسه ولی آدم به آدم می رسه. هندسه مثلث رو دید بهش قطر نداد. اقلیدس نقطه رو دید بهش خط نداد. یه مستطیل واست بسازم که صد تا مربع توش در بیاد. مثلثی به مثلثی می رسه میگه برو قطر نداری. سه شنبه 10 بهمن 1391برچسب:, :: 1:46 :: نويسنده : نا شناس
همواره افرادی بر این عقیده بوده اند که موسیقی از دسته ی علوم ریاضی بشمار میرود و گرچه نوع بیان موسیقی و ریاضی با یکدیگر متفاوت بوده اما روح و حقیقتی که در موسیقی وجود دارد، در ریاضیات قابل مشاهده است؛ بنابراین همواره وجود داشته اند افرادی که بخواهند ریاضیات و موسیقی را به زبان دیگری تعریف کرده و یا از این علوم قدرتمند جهت غنا بخشیدن به دیگری استفاده کنند. آن طور که در تاریخ آمده شروع بررسی موسیقی از دیدگاه ریاضی به یونان باستان بازمیگردد و فیثاغورثیان در پانصد سال قبل از میلاد، اولین افرادی بودند که فواصل موسیقی را متناسب با اعداد بیان کرده و ارتباط موسیقی و ریاضیات را توجیه کردند.
سه شنبه 10 بهمن 1391برچسب:, :: 1:36 :: نويسنده : نا شناس
واژه فرکتال درسال 1976 توسط رياضيدان لهستاني به نام بنوئيت مندلبرات وارد دنياي رياضيات شد. واژه فركتال به معناي سنگي است كه به شكل نامنظم شكسته شده باشد.
فراکتال هانظريه ي بي نظمي (آشوب) يک مفهوم رياضياتي محسوب ميشود که شايد نتوان خيلي دقيق آن را تعريف کرد، اما ميتوان آن را نوعي اتفاقي بودن همراه با قطعيت دانست؛ قطعيت آن به خاطر آن است که بينظمي دلايل دروني دارد و به علت اختلالات خارجي رخ نميدهد، اتفاقي بودن آن هم به دليل آن است که رفتار بينظمي، بيقاعده و غير قابل پيشبيني است. اين تئوري که در حيطه علوم تجربي، رياضيات، رفتار شناسي، مديريت، جامعه شناسي و ... وارد شده و باعث تغيير در نوع ديدگاه بشر به حل مسائل غير قابل پيشبيني شدهاست. انگاره اصلي و کليدي تئوري آشوب اين است که در هر بينظمي، نظمي نهفتهاست. به اين معنا که نبايد نظم را تنها در يک مقياس جستجو کرد و پديدهاي که در مقياس محلي، کاملاً تصادفي و غير قابل پيشبيني به نظر ميرسد، چه بسا در مقياس بزرگتر کاملاً پايا و قابل پيشبيني باشد.
پيوندها
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||